１， ２次元信号とスペクトル

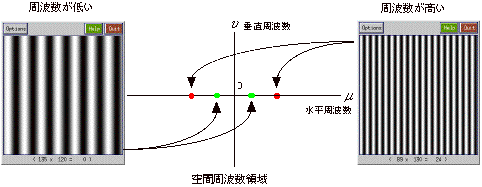
下記のような１次元の信号は時間波形を眺めることで，その特徴をとらえることができます。信号の時間波形を表示することは，信号を時間領域で表現していることになりますが，周波数領域でも信号を表現することができます。信号の周波数領域での特徴は周波数特性と呼ばれ，振幅特性（振幅スペクトル）と位相特性（位相スペクトル）とで表現されます。図の下部に示す１次元信号の振幅スペクトルの例では，信号がf₀ Hzの単一の周波数成分から成り立っていることを示しています。位相スペクトルは，信号が基準時刻からどれだけ進みあるいは遅れているかを示すものです。時間領域表現と周波数領域表現とでは，その表現方法は異なりますが，見る視点が異なるだけで，同じ信号を眺めていることになります。すなわち，情報としては等価なものですので，時間領域で表現されたものを周波数領域へ，またその逆の変換を行うことが可能です。

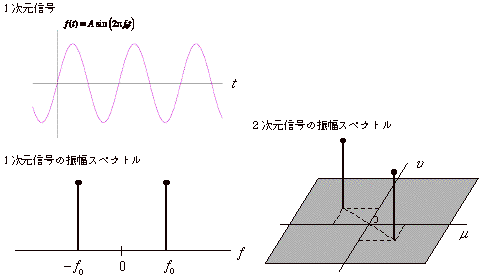
１次元信号の場合は，そのスペクトルは横軸に周波数をとった２次元の図で表現することができますが，画像のような２次元信号の場合は，下記に示すように，水平（m）と垂直（u）の２つの周波数成分が関係するので，スペクトルは３次元の図で表現されることになります。しかし，３次元の図では理解が容易ではないので，図を上側から眺め，スペクトル強度の大きさを濃淡で示す手法が用いられます。強度の大きい部分は白く，小さい部分は黒く表示するようにすれば，２次元の図として表示することが可能になります。

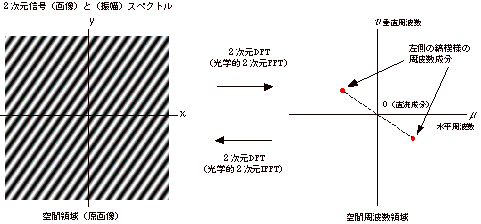
２次元信号の例として，斜め縞の画像を下記に示します。濃淡が正弦波状に変化する縞模様となっています。この画像を空間周波数領域で眺めると，下記のような位置に成分が現れます。

時間領域で表現されたものを周波数領域へ変換するには，２次元離散的フーリエ変換（DFT）が，その逆の変換には２次元離散的フーリエ逆変換（IDFT）がそれぞれ用いられます。実際には，中央部に直流成分を配置した光学的フーリエ変換がFFTを用いて行われます。

周波数の高低と空間周波数領域での成分配置